Vectors

Routines for working with vectors These routines can be used with vectors, as well as with matrices containing a vector in each row.

Functions

• vector.angle() … Angle between two vectors

• vector.GramSchmidt() … Gram-Schmidt orthogonalization of three points

• vector.normalize() … Normalization of a vector

• vector.project() … Projection of one vector onto another

• vector.plane_orientation() … Orientation of plane defined by three points

• vector.q_shortest_rotation() … Quaternion indicating the shortest rotation from one vector into another.

• vector.rotate_vector() … Rotation of a vector

• vector.target2orient() … Convert target location into orientation angles

Details

Routines for working with vectors These routines can be used with vectors, as well as with matrices containing a vector in each row.

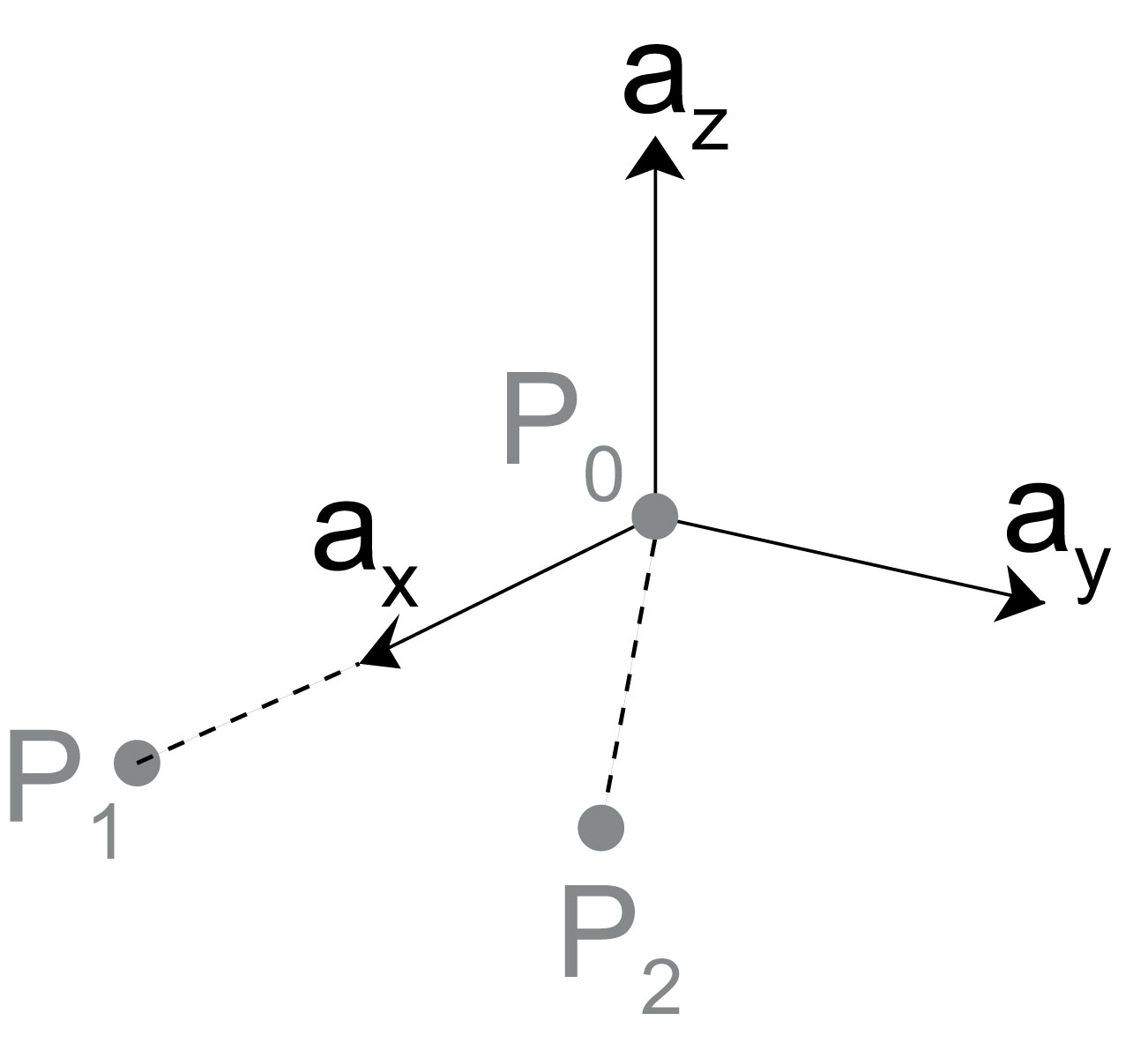
vector.GramSchmidt(p0, p1, p2)

Gram-Schmidt orthogonalization

Parameters:

• p0 (array (3,) or (M,3)) – coordinates of Point 1

• p1 (array (3,) or (M,3)) – coordinates of Point 2

• p2 (array (3,) or (M,3)) – coordinates of Point 3

Returns:

Rmat – flattened rotation matrix

Return type:

array (9,) or (M,9)

Example

>>> P0 = np.array([[0, 0, 0], [1,2,3]])
>>> P1 = np.array([[1, 0, 0], [4,1,0]])
>>> P2 = np.array([[1, 1, 0], [9,-1,1]])
>>> GramSchmidt(P0,P1,P2)
array([[ 1.        ,  0.        ,  0.        ,  0.        ,  1.        ,
     0.        ,  0.        ,  0.        ,  1.        ],
   [ 0.6882472 , -0.22941573, -0.6882472 ,  0.62872867, -0.28470732,
     0.72363112, -0.36196138, -0.93075784, -0.05170877]])

Notes

The flattened rotation matrix corresponds to

\[\mathbf{R} = [ \vec{e}_1 \, \vec{e}_2 \, \vec{e}_3 ]\]

vector.angle(v1, v2)

Angle between two vectors

Parameters:

• v1 (array (N,) or (M,N)) – vector 1

• v2 (array (N,) or (M,N)) – vector 2

Returns:

angle – angle between v1 and v2

Return type:

double or array(M,)

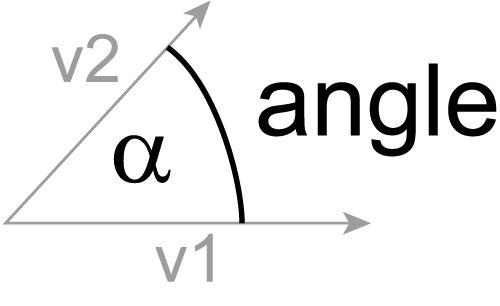
Example

>>> v1 = np.array([[1,2,3],
>>>       [4,5,6]])
>>> v2 = np.array([[1,0,0],
>>>       [0,1,0]])
>>> skinematics.vector.angle(v1,v2)
array([ 1.30024656,  0.96453036])

Notes

\[\alpha =arccos(\frac{\vec{v_1} \cdot \vec{v_2}}{| \vec{v_1} | \cdot | \vec{v_2}|})\]

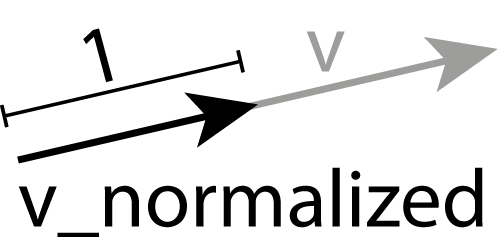
vector.normalize(v)

Normalization of a given vector (with image)

Parameters:

v (array (N,) or (M,N)) – input vector

Returns:

v_normalized – normalized input vector

Return type:

array (N,) or (M,N)

Example

>>> skinematics.vector.normalize([3, 0, 0])
array([[ 1.,  0.,  0.]])

>>> v = [[np.pi, 2, 3], [2, 0, 0]]
>>> skinematics.vector.normalize(v)
array([[ 0.6569322 ,  0.41821602,  0.62732404],
   [ 1.        ,  0.        ,  0.        ]])

Notes

\[\vec{n} = \frac{\vec{v}}{|\vec{v}|}\]

vector.plane_orientation(p0, p1, p2)

The vector perpendicular to the plane defined by three points.

Parameters:

• p0 (array (3,) or (M,3)) – coordinates of Point 0

• p1 (array (3,) or (M,3)) – coordinates of Point 1

• p2 (array (3,) or (M,3)) – coordinates of Point 2

Returns:

n – vector perpendicular to the plane

Return type:

array (3,) or (M,3)

Example

>>> P0 = np.array([[0, 0, 0], [1,2,3]])
>>> P1 = np.array([[1, 0, 0], [4,1,0]])
>>> P2 = np.array([[1, 1, 0], [9,-1,1]])
>>> plane_orientation(P0,P1,P2)
array([[ 0.        ,  0.        ,  1.        ],
       [-0.36196138, -0.93075784, -0.05170877]])

Notes

\[\vec{n} = \frac{ \vec{a} \times \vec{b}} {| \vec{a} \times \vec{b}|}\]

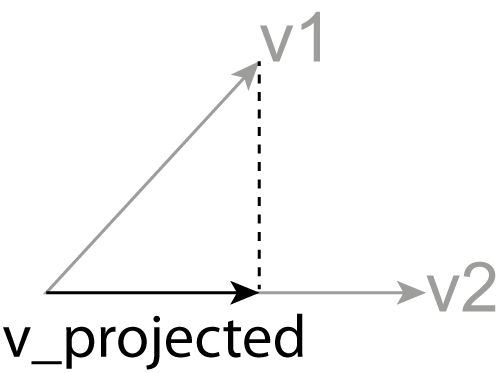
vector.project(v1, v2, projection_type='1D')

Project one vector onto another, or into the plane perpendicular to that vector.

Parameters:

• v1 (array (N,) or (M,N)) – projected vector

• v2 (array (N,) or (M,N):) – target vector

• projection_type (scalar) –

  Has to be one of the following:

  • 1D … projection onto a vector (Default)

  • 2D … projection into the plane perpendicular to that vector

Returns:

v_projected – projection of v1 onto v2

Return type:

array (N,) or (M,N)

Example

>>> v1 = np.array([[1,2,3],
>>>       [4,5,6]])
>>> v2 = np.array([[1,0,0],
>>>       [0,1,0]])
>>> skinematics.vector.project(v1,v2)
array([[ 1.,  0.,  0.],
   [ 0.,  5.,  0.]])

Notes

\[ \begin{align}\begin{aligned}\vec{n} = \frac{ \vec{a} }{| \vec{a} |}\\\vec{v}_{proj} = \vec{n} (\vec{v} \cdot \vec{n})\\\mathbf{c}^{image} = \mathbf{R} \cdot \mathbf{c}^{space} + \mathbf{p}_{CS}\end{aligned}\end{align} \]

Note that the orientation of the 2D projection is not uniquely defined. It is chosen here such that the y-axis points up, and one is “looking down” rather than “looking up”.

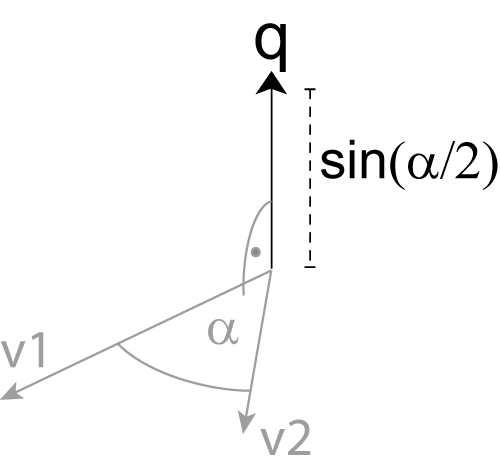
vector.q_shortest_rotation(v1, v2)

Quaternion indicating the shortest rotation from one vector into another. You can read “qrotate” as either “quaternion rotate” or as “quick rotate”.

Parameters:

• v1 (ndarray (3,)) – first vector

• v2 (ndarray (3,)) – second vector

Returns:

q – quaternion rotating v1 into v2

Return type:

ndarray (3,)

Example

>>> v1 = np.r_[1,0,0]
>>> v2 = np.r_[1,1,0]
>>> q = qrotate(v1, v2)
>>> print(q)
[ 0.          0.          0.38268343]

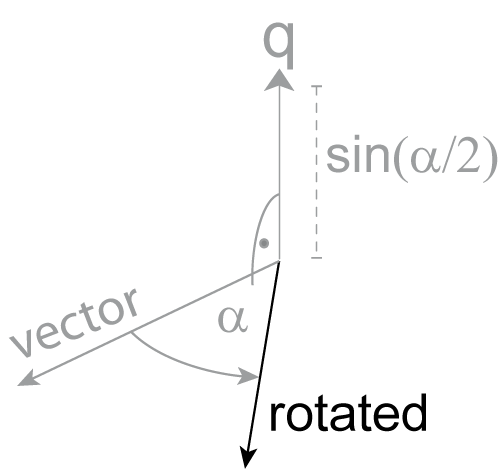
vector.rotate_vector(vector, q)

Rotates a vector, according to the given quaternions. Note that a single vector can be rotated into many orientations; or a row of vectors can all be rotated by a single quaternion.

Parameters:

• vector (array, shape (3,) or (N,3)) – vector(s) to be rotated.

• q (array_like, shape ([3,4],) or (N,[3,4])) – quaternions or quaternion vectors.

Returns:

rotated – rotated vector(s)

Return type:

array, shape (3,) or (N,3)

Notes

\[q \circ \left( {\vec x \cdot \vec I} \right) \circ {q^{ - 1}} = \left( {{\bf{R}} \cdot \vec x} \right) \cdot \vec I\]

More info under http://en.wikipedia.org/wiki/Quaternion

Examples

>>> mymat = eye(3)
>>> myVector = r_[1,0,0]
>>> quats = array([[0,0, sin(0.1)],[0, sin(0.2), 0]])
>>> quat.rotate_vector(myVector, quats)
array([[ 0.98006658,  0.19866933,  0.        ],
       [ 0.92106099,  0.        , -0.38941834]])

>>> quat.rotate_vector(mymat, [0, 0, sin(0.1)])
array([[ 0.98006658,  0.19866933,  0.        ],
       [-0.19866933,  0.98006658,  0.        ],
       [ 0.        ,  0.        ,  1.        ]])

vector.target2orient(target, orient_type='quat')

Converts a target vector into a corresponding orientation. Useful for targeting devices, such as eyes, cameras, or missile trackers. Based on the assumption, that in the reference orientation, the targeting device points forward.

Parameters:

• target (array (3,) or (N,3)) – Input vector

• orient_type (string) –

  Has to be one the following:

  • Fick … Rz * Ry

  • nautical … same as “Fick”

  • Helmholtz … Ry * Rz

  • quat … quaternion

Returns:

orientation – Corresponding orientation For rotation matrices, same sequence as the matrices [deg]. For quaternions, the quaternion vector.

Note that the last column of the sequence angles, and the first column of the quaterion, will always be zero, because a rotation about the line-of-sight has no effect.

Return type:

array (3,) or (N,3)

Example

>>> a = [3,3,0]
>>> b = [5., 0, 5]
>>> skinematics.vector.target2orient(a)
[ 0.          0.          0.38268343]

>>> skinematics.vector.target2orient([a,b])
[[ 0.          0.          0.38268343]
 [ 0.         -0.38268343  0.        ]]

>>> skinematics.vector.target2orient(a, orient_type='nautical')
[ 45.  -0.   0.]