When analyzing survival times, different problems come up than the ones discussed so far. One question is how do we deal with subjects dropping out of a study. For example, assume that we test a new cancer drug. While some subjects die, others may believe that the new drug is not effective, and decide to drop out of the study before the study is finished. A similar problem would be faced when we investigate how long a machine lasts before it breaks down.
Survival Probabilities¶
Kaplan-Meier survival curve¶
A clever way to deal with these problems is described in detail in . First, the time is subdivided into small periods. Then the likelihood is calculated that a subject survives a given period. The survival probability is given by
where \(p_k\) is the probability to survive period \(k\); \(r_k\) is the number of subjects still at risk (i.e. still being followed up) immediately before the \(k^{th}\) day, and \(f_k\) is the number of observed failures on the day \(k\). The curve describing the resulting survival probability is called life table, survival curve, or Kaplan-Meier curve (see Figure [fig:SurvivalCurve]).
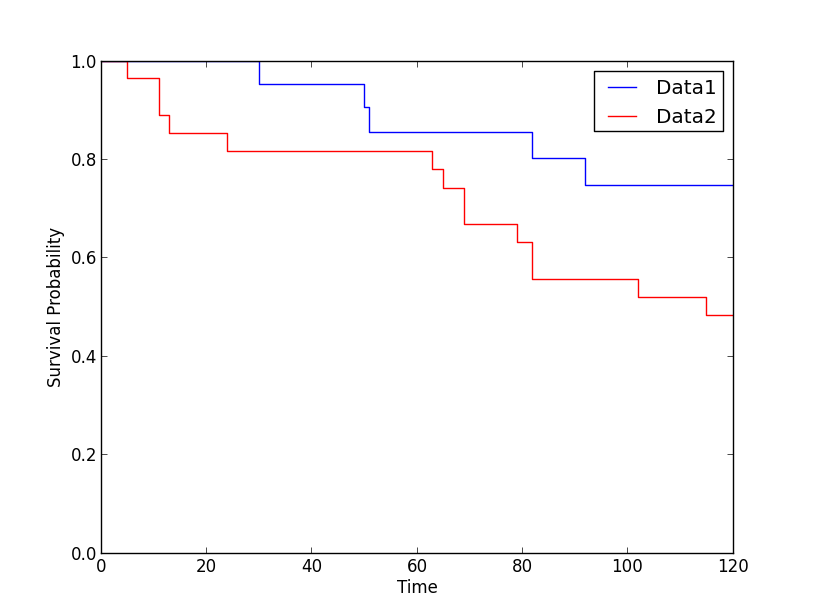
Survival curve corresponding to a motion sickness experiment, described in more detail in [Altman(1999)], chapter 13
Note that the survival curve changes only when a “failure” occurs, i.e. when a subject dies. Censored entries, describing either when a subject drops out of the study or when the study finishes, are taken into consideration at the “failure” times, but otherwise do not affect the survival curve.
Comparing Survival Curves in Two Groups¶
The most common test for comparing independent groups of survival times is the logrank test. This test is a non-parametric hypothesis test, testing the probability that both groups come from the same underlying population. Since to my knowledge this test is not yet implemented in a Python library, I have included an implementation based on the equations given by (see program [py:survival]).
To explore the effect of different variables on survival, more advanced methods are required. The Cox regression model introduced by Cox in 1972 is used widely when it is desired to investigate several variables at the same time. For details, check or other statistic textbooks.